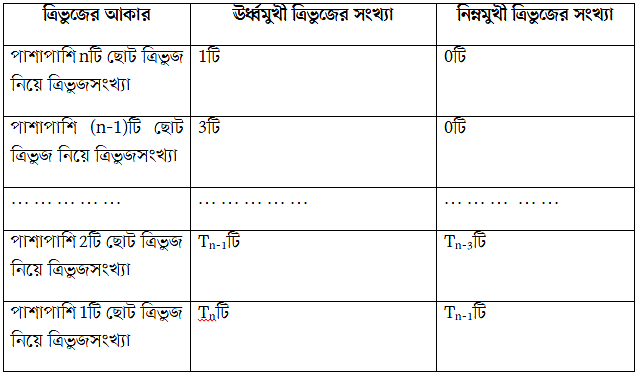
উপরিউক্ত ছক থেকে মোট ত্রিভুজ হয় 1+3+6+10+6+1 = 27টি। এখন, ছকটি থেকে আমরা একটি প্যাটার্ন নির্ণয় করার চেষ্টা করি। ধরি, বৃহত্তম ত্রিভুজটির ভেতরের পাশাপাশি ছোট ত্রিভুজের সর্বোচ্চ সংখ্যা n।
এখানে ঊর্ধ্বমুখী ত্রিভুজের সংখ্যা ও নিম্নমুখী ত্রিভুজের সংখ্যার ধারা দুটি সমন্বয় করলে নির্ণেয় সমষ্টি হবে {n(n+2)(2n+1)}/8 ; যেখানে বৃহত্তম ত্রিভুজটির ভেতরের পাশাপাশি ছোট ত্রিভুজের সর্বোচ্চ সংখ্যা n। পুরো প্রমাণটি পরবর্তী কোনো পর্বে আলোচনা করব।
(iv) চিত্রে বৃহত্তম ত্রিভুজটির ভেতরের পাশাপাশি ছোট ত্রিভুজের সর্বোচ্চ সংখ্যা 4। সুতরাং, মোট ত্রিভুজসংখ্যা হবে 4(4+2){(2×4)+1}/8 = 27টি। এখানে বলা বাহুল্য, ফলাফল দশমিক নম্বর হলে, নিচের দিকের পূর্ণসংখ্যাই হবে নির্ণেয় ত্রিভুজসংখ্যা। যেমন, ফলাফল 20.11 হলে নির্ণেয় ফলাফল হবে 20, আবার ফলাফল 20.9 হলেও নির্ণেয় ফলাফল 20 হবে।
আশা করছি, ওপরের সূত্রটি তোমরা বুঝতে পেরেছ।তো আপনমনে গণিত চর্চা করতে থাকো। দেখা হবে অন্যদিন, নতুন কোনো গাণিতিক বিষয় নিয়ে।






No comments:
Post a Comment